Regression

Regression이란?

여러 개의 독립 변수에서 하나의 종속 변수를 유도해 내는 것을 말한다.

 

Linear Regression의 일반식은 다음과 같다.

$$r = f(x) + \varepsilon  (X = (x^t, r^t)^N_{t=1}, f(x^t) = w^Tx^t )$$

• $x$ : 독립 변수
• $r$ :  종속 변수. 즉, 맞추고자 하는 real value
• $f(x)$ : linear regression을 통해 예측한 예측값(추정량 - estimator). 즉, $y^t$라고 볼 수 있다.

위의 식에서 $x^t$는 t번째 독립 변수로, $x^t = (x^t_{1}, x^t_{2}, ... , x^t_{k})$와 같은 Feature $x^t_{j}$의 결합이다.

또한 $w^T$는 parameter로, $w^T = (w_{1}, w_{2}, ... , w_{k})$와 같은 parameter를 의미한다.

 

여기서 parameter $\theta$(위의 $w^T$와 동일)를 가질 경우 추정량(estimator) $g(x|\theta)$(위에서 말한 $f(x)$와 동일)를 가진다고 하자.

$\varepsilon$은 잔차(residual)로, $\varepsilon$ ~ $N(0,\sigma^2)$인 정규 분포를 따른다면,

$$p(r|x,\theta) \sim N(g(x|\theta), \sigma^2)$$

라는 분포를 가질 것이다.

 

이를 가장 쉬운 형태인 linear regression(선형 회귀) 형태의 그래프로 나타내어 이해해 보자.

 

linear regression의 경우 parameter $\theta$가 기울기 추정량$w_1$과 절편 추정량 $w_0$를 가진다 했을 때,

특정 점 $x^t$에서의 estimator(추정량) $g(x|\theta)$는 $w_1x^t + w_0$의 일차식을 가지게 될 것이다.

linear model에서 x1에서의 gaussian distribution of y

위의 그래프에서 점 $x^t$에서의 예측값(expected value)은 $E[y^t|x^t] = w_1x^t + w_0$로 표현 가능하고,

$E[y^t|x^t]$와 real value 사이의 차는 $\varepsilon$ 즉, residual을 더해주면

$$r^t = w_1x^t + w_0 + \varepsilon$$

 

와 같은 식이 완성된다.

 

 

Log Likelihood

선형 회귀에서 n개의 점이 있으며 각 점은 $(x^t, r^t)$라는 점을 가진다고 했을 때,

log likelihood를 구해보자.

$$L(\theta|X) = log\prod^{N}_{t=1}p(D|\theta) = log\prod^{N}_{t=1}p(r^t| x^t, \theta)\tag{1}$$

 

이와 같이 나오게 된다

 

앞서 언급했던 것과 같이 $p(r|x,\theta)$ ~ $N(g(x|\theta), \sigma^2)$라는 정규 분포를 따라가게 되므로

각 데이터 포인트의 $p(r^t| x^t, \theta)$를 정규 분포의 확률밀도함수로 표현해주게 된다면 다음과 같다.

$$p(r^t| x^t, \theta) = \frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{(r^t-(w_1x^t + w_0))^2}{2\sigma^2}] \tag{2}$$

 

(2) 식을 (1) 식에 정리하여 대입하게 되면 다음과 같은 식으로 정리된다.

$$L(\theta|X) = \sum^{N}_{t=1}log\frac{1}{\sqrt{2\pi}\sigma}exp[\frac{2\sigma^2}{[r^t - g(x^t|\theta)]^2}]$$

$$= -\frac{1}{2\sigma^{2}}\sum^{N}_{t=1}\varepsilon^2 - \frac{N}{2}log(2\pi\sigma^{2})\tag{3}$$

 

여기서 $\sum^{N}_{t=1}\varepsilon^2 = RSS(w) = ||\varepsilon||^{2}$와 같은 l2 norm으로 표현 가능하다.

RSS는 Sum of Squared Error(N으로 나누면 Mean Squared Error)이라고 불린다.

 

(3) 식에서 $\varepsilon$와 무관한 항을 지워서 정리해준다면

$$E(\theta|X) = \frac{1}{2}\sum^{N}_{t=1}[r^t - g(x^t|\theta)]^2 = \frac{1}{2}\sum^{N}_{t=1}\varepsilon^2$$

 

이렇듯, linear regression은 다음과 같은 RSS(Error이기에 $E(\theta|X)$로 표시했다)를 minimize하는 동시에

Likelihood 값이 maximize되는 parameter W(동시에 $\theta$값)을 찾는 것이다.

 

 

행렬식 사용하여 수식 풀기

앞서 linear regression은 estimator이 다음과 같이 표현됨을 확인했다.

$$g(x^t|w_1, w_0) = w_1x^t + w_0$$

 

이를 앞선 expected value 식($E(\theta|X) = \frac{1}{2}\sum^{N}_{t=1}[r^t - g(x^t|\theta)]^2$)에 대입한다고 생각해보자

식을 전개하면

$$\sum^{N}_{t=1}[r^t - g(x^t|\theta)]^2 = \sum^{N}_{t=1}[{r^t}^2 - 2r^tg(x^t|\theta) + g(x^t|\theta)^2]$$

 

위 식을 간단하게 만들기 위해 행렬을 사용하자.

$$\sum^{N}_{t=1}r^t = Nw_0 + w_1\sum^{N}_{t=1}x^t$$

$$\sum^{N}_{t=1}r^tx^t = w_0\sum^{N}_{t=1}x^t + w_1\sum^{N}_{t=1}(x^t)^2$$

이므로, 이를 행렬로 표현한다면

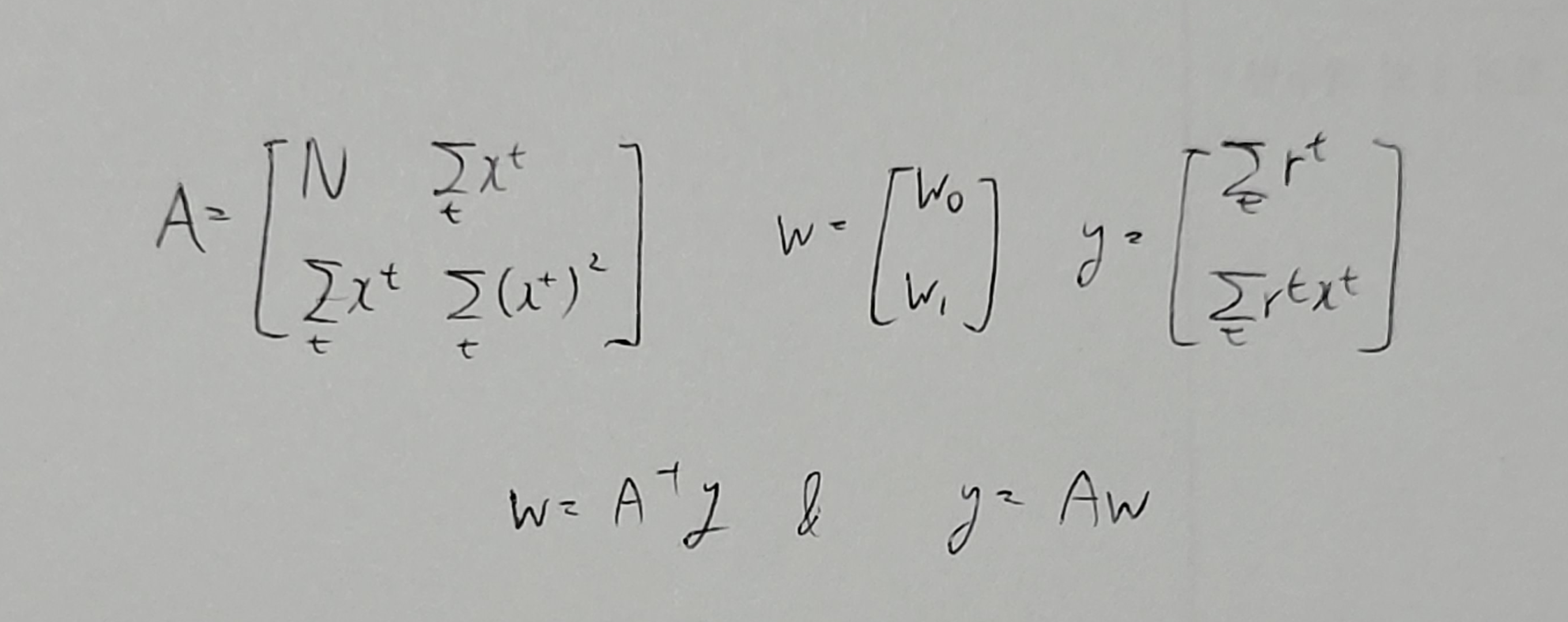
로 표현된다.

 

 

Polynomial Regression

Polynomial Regression의 경우 1개의 feature만 가지고 있었던 linear regression과 달리 2개 이상인 k개의 feature을 가지고 있다.

 

$$g(x^t | w_k, ... , w_2, w_1, w_0) = w_k (x^t)^k + ... w_2 (x^t)^2 + w_1x^t + w_0$$

 

이를 또 행렬로 나타내 준다면

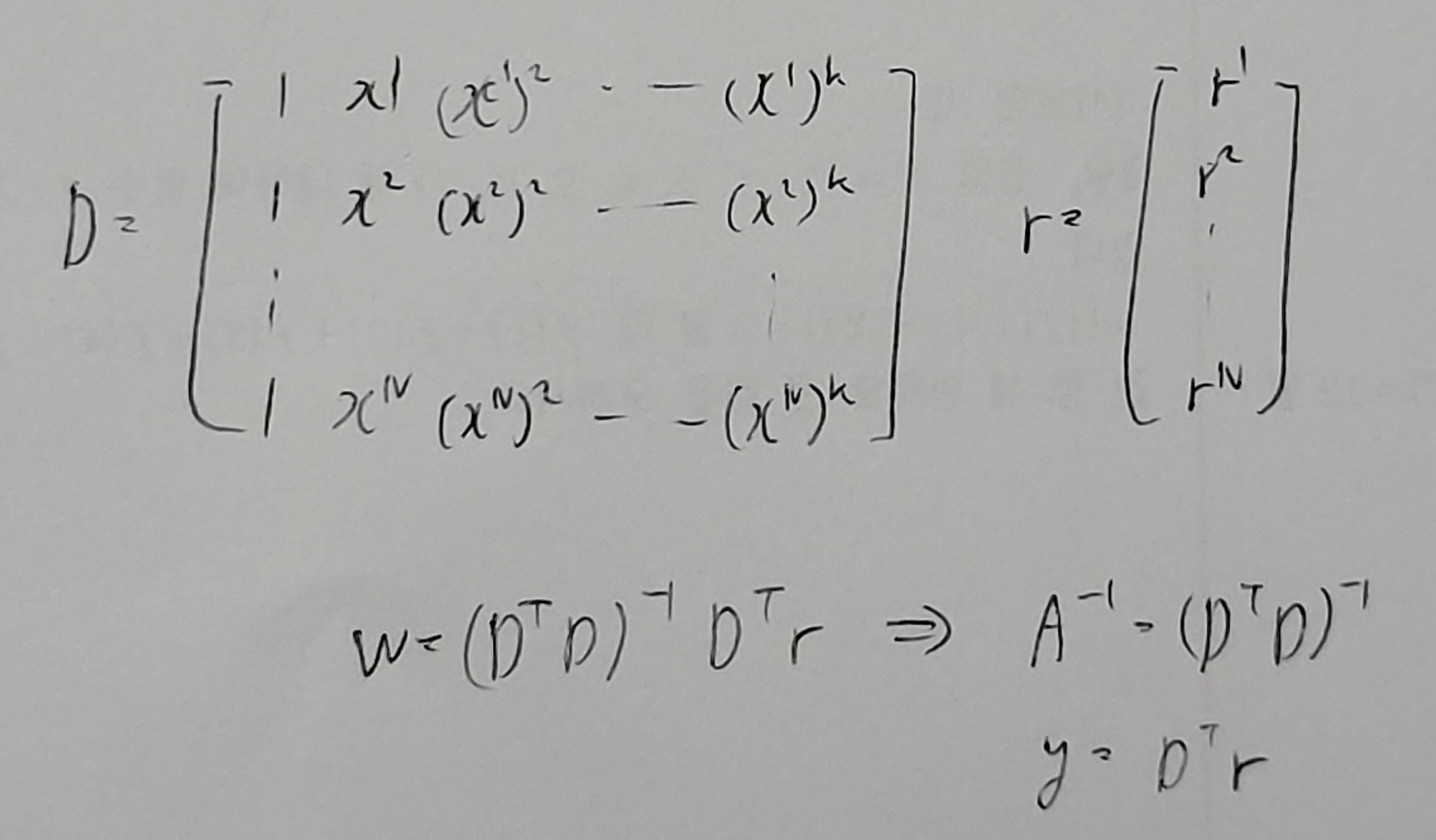
와 같은 식으로 표현된다.

 

출처

https://shurain.net/personal-perspective/linear-regression/

Linear Regression — Sungjoo Ha

https://shurain.net/personal-perspective/linear-regression/

Linear Regression — Sungjoo Ha

https://process-mining.tistory.com/125

Linear Regression이란? (선형회귀란?, linear regression과 MLE)